2023(2024수능) 10월 교육청 모의고사 13번 문제풀이

우선 곡선 세개와 직선하나가 그래프에 표현되어 있는데, 그중 직선과 교점관계를 가지고 있는 곡선이 두 개인 것으로 확인할 수 있다. a+k의 값을 구하라고 하였으므로 PR과 QR의 길이를 이용하여 세점 PRQ 간의 관계를 구하고 직선과 곡선의 교점임을 이용하여 좌표값을 정확히 파악하는 것으로 이루어진 문제인 것으로 보인다.

PR과 RQ의 길이가 같으므로 이등변삼각형으로 생각해서 PQ에 수선의 발을 내려 관계를 파악할 생각을 해볼 수도 있겠지만 데카르트 좌표계에서는 좌표가 x,y축의 방향의 기저벡터(1,0),(0,1)로 표현되어있는 것이므로 점간의 관계를 파악할 때 x,y축에 맞게 수직을 내려서 파악하는게 편해서 다른 방식을 생각해볼 필요가 있다.
두 곡선과 직선간의 관계를 먼저 살펴보자. 직선의 기울기가 -2이므로 x변화량이 1일때 y변화량이 -2임을 이용하여 점P에서 RQ에 내린 수선의 발을 H라고 했을 때 HQ를 m이라고 하면 PH는 2m, RM은 5-m으로 표현할 수 있다. 그러고나서 삼각형 PRH에서 피타고라스정리를 이용하여 m의 값을 구할 수가 있다.

m의값은 2가 나오므로 점간의 관계인 PH=4, HQ=2, HR=3임을 바로 파악할 수가 있다.
이제부터 풀이가 오래 걸릴 수가 있는 상황이 생길 수가 있는데, P의 좌표를 두고 들어가는 풀이가 그런 상황인 것이다. 만약 여기서 P좌표를 ( α,-2α+k)로 두고 들어갔으면 방정식이 지수와 다항식이 섞여서 나오므로 방정식을 푸는데 배운대로 풀 수 있는 방법은 없고 공통부분을 찾아 지워가는 식으로 풀어야하는 경우가 생긴다. 지수로그 방정식을 배울 때 지수는 지수끼리 로그는 로그끼리,다항식은 다항식끼리 방정식을 푸는 것을 배웠지 그것들이 섞이는 것에 대해 배우지 않는다. 따라서 P좌표를 잡을 때 (α, 2^(α+1) +1)로 잡아야 지수방정식으로 풀 수 있는 것이다.
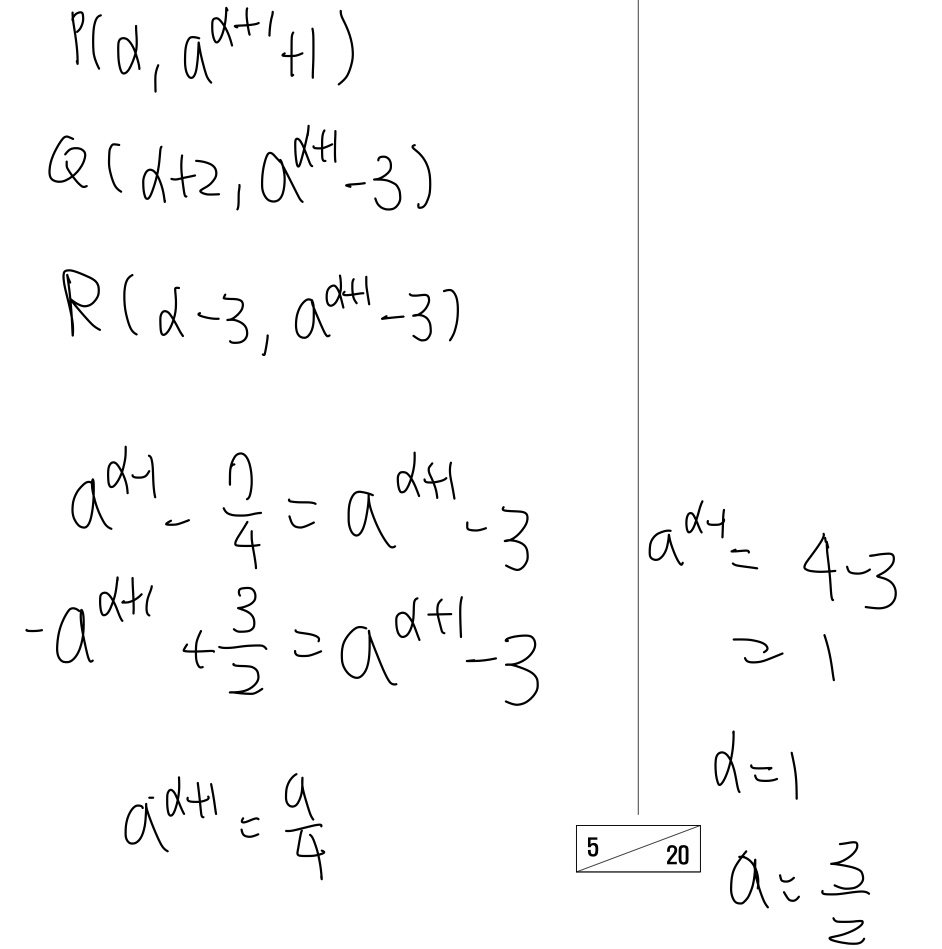
직선과 두 곡선의 교점 관계일 때 직선의 기울기를 알고 있거나 교점간의 거리를 알고 있으면 생각해볼 수 있는 풀이가 있다. 함수의 평행이동이다.
P가 지나는 지수함수에서 (+2,-4)만큼 평행이동한 함수와 Q를 지나는 지수함수의 교점을 Q, P가 지나는 지수함수에서 (-3,-4)만큼 평행이동한 함수와 R를 지나는 지수함수의 교점을 R 라고 생각해보는 것이다. 좌표를 평행이동하는 것이 아닌 함수자체를 평행이동시켜 함수간의 교점방정식을 구하는 아이디어다. 이렇게 식을 전개하게 되면 다항식과 지수가 포함되어있는 방정식은 절대 나올 수 없으므로 자연스럽게 지수방정식을 푸는 것으로 넘어가게 되는 것이다. 이 때 조심해야할 점은 두개의 방정식은 연립방정식의 관계가 아니라는 점이다. 하나의 방정식은 Q에 대한 방정식, 다른 하나의 방정식은 R에 대한 방정식이므로 이 두개의 방정식을 연계시키려면 R Q간의 관계를 하나 찾아야할텐데, R에서 Q로 평행이동한 방정식은 쓰지 않았으므로 이 둘간의 관계인 x좌표 차이가 5인 것 하나만 더 쓰면 쉽게 방정식을 풀어나갈 수 있을 것이다.

누구나 시간만 주면 답은 구할 수 있는 문제이지만 생각해 볼 거리가 많다. 점 간의 관계를 찾을 때 기저벡터에 맞게 찾고 있는가. 좌표를 구할 때 방정식을 풀 수 있도록 잘 잡아놓고 풀었는가. 함수의 평행이동으로 교점관계를 구할 생각을 해볼 수 있는가 정도 될 것인데, 이 정도만 잘 파악해놓고 문제풀이에 들어갔으면 막히지 않고 빠르게 넘어갈 수 있었던 것이다.