지수로그함수 그래프 문제에서 많이 나오는 개념인데, 곡선과 직선이 그래프에 표현되어 있을 때 식으로 접근하는 것이 아닌 함수의 해석을 통해 기하적인 접근(그래프 풀이)을 할 수 있는 시각을 가져보라는 것이다.
우선 제일 간단한 상황을 생각해보자. 어떤 함수 f(x)와 일차함수(직선의 방정식) g(x)가 두 점에서 만난다고 했을 때 두 점의 관계를 알아야하는 상황이라면 우선 f(x)=g(x)를 통해 식 정리를 하여 근의 관계를 파악하는 식으로 식풀이를 생각해볼 수가 있다. 만약 f(x)가 다항함수라면 식으로 푸는 방식은 적합하다고 볼 수 있다. '다항식=다항식'이므로 인수분해하는 식으로 식정리를 할 수도 있고 근과 계수관계를 이용할 수도 있기 때문이다.
지수로그함수 그래프 문제에서 많이 나오는 개념이라고 말한 이유가 여기에 있다. 만약 f(x)가 다항식이 아닌 지수함수나 로그함수라면? '지수로그함수=다항식' 의 방정식 꼴이 나오므로 이를 보편적으로 정리할 수 있는 방법을 우리는 고등교육과정에서 배우지 않는다. 지수=지수, 로그=로그 방정식 꼴에 대한 것들을 지수로그방정식 단원에서 배우지 지수,로그,다항식이 섞여있는 방정식을 정리하는 것에 대해서는 배우지 않는다는 것이다. 물론 어떻게 공통되는 어떤 것들을 치환해서 푸는 식으로 풀면 방정식을 푸는 방식으로 접근할 수 있기는 하지만 항상 이렇게 풀 수 있는 것이 아니기도 하고 공통되는 꼴을 찾지 못하는 경우도 나오기 때문에 배우지 않은 방정식을 풀 때 식이 도는 듯한 느낌이 들면서 풀지 못하는 경험을 수학공부를 했던 누구나 해봤을 것이다.
그렇게 때문에 이런 상황에서는 식에 대한 접근을 하는 것이 아닌 그래프 해석으로 접근을 하는 것이 중요하다. 직선의 방정식 기울기를 이용하는 것이 핵심 포인트인데, 기울기를 통해 곧 x,y 축에 각각 평행한 선분을 가지고 있는 직각삼각형의 삼각비를 확인할 수 있고, 이를 통해 두 점간의 관계는 식을 풀지 않아도 삼각비로 알 수 있다는 것이다.
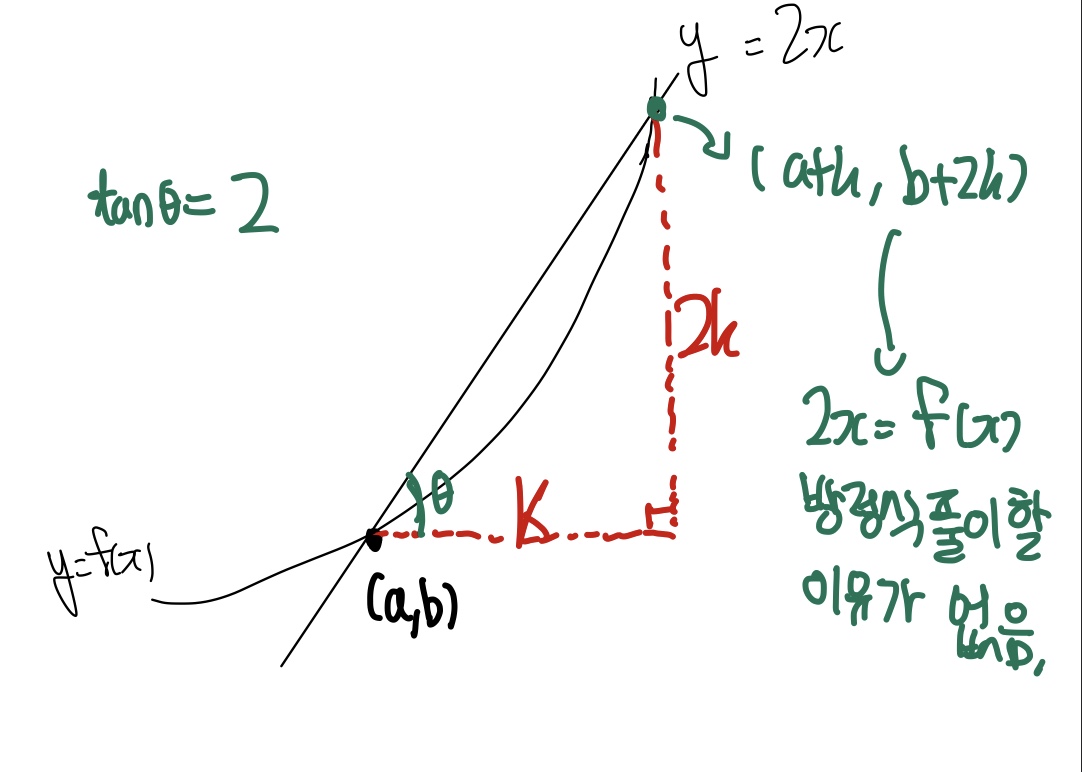
최근에 보았던 2023 10월 교육청 10번 문제를 예시를 들어보겠다.

해당문제는 그래프형태가 다항식과 다항식의 교점으로 되어있으므로 식으로 접근해볼 생각은 해야한다. 근을 직접 찾을 수 있을 뿐만 아니라 근과계수 관계를 이용할 수도 있고 최고차항이 2차라면 판별식이라는 툴도 이용해볼 수 있기 때문이다. 하지만 이 문제를 식으로'만' 접근하려고 했으면 좌표값을 구하고 거리공식까지 구해야하는 계산적으로 힘든 과정을 겪어야하는 상황이 생겨버린다.

이 때문에 그래프 해석을 해볼 필요가 있다. 다항식인 것을 떠나 곡선과 직선의 관계에 대한 그래프로 되어있으므로 직선의 기울기를 이용해볼 생각을 하는 것이다. 일차함수의 기울기는 t이므로 삼각비를 알 수 있게 되고 AB길이를 x좌표 차이나 y좌표 차이 중 하나만 알게 되어도 구할 수 있게 되는 상황인 것이다. 따라서 식을 통해 두 근의 근과 계수관계를 이용하여 x좌표차이를 구하고 거기에 삼각비를 적용하면 그게 구하고자하는 AB길이인 것이다.

한 곡선과 직선이 만났을 때는 이렇게 직선의 기울기를 이용하여 교점관계를 파악해보는 생각을 해볼 수가 있다.
평행이동 돼 있는 관계의 두 곡선과 직선이 만났을 때는 어떨까? 이 때도 평행이동의 개념을 활용해볼 수가 있을텐데, 이에 대한 내용은 다음 글에 정리해보겠다.
'수능수학 실전개념 > 함수의 해석 및 조작' 카테고리의 다른 글
| 함수의 배수변환, 함수의 해석 총정리 (0) | 2023.12.15 |
|---|---|
| 함수의 대칭이동 - 대칭은 합이 일정하다 (1) | 2023.11.21 |
| 함수의 평행이동(3) - 두 곡선과 직선의 관계해석 (0) | 2023.11.05 |
| 함수의 평행이동(1) - 좌표의 평행이동과는 왜 반대부호를 가지는가. (0) | 2023.10.31 |